Randomized Response はアンケートの回答をランダム化することで、個人の回答は伏せつつ平均などの統計量を得る手法の1つ。
前回までの記事で、ランダム化された回答から真の割合を最尤推定とベイズ推定(ギブスサンプリング)で推定する方法とそれらの実験を紹介した。今回は同じベイズ推定でも変分ベイズによる推論を行ってみる。
Randomized Response のギブスサンプリングによる推論までは普通に論文が見つかるが、変分ベイズ推論は探した範囲では見つけられなかったので、頑張って導出してみる。
Collapsed Variational Bayes 推論
記法は前回と同様。
通りの選択肢を持つ質問
に対する回答を確率変数
で表す。
回答者は真の回答 を知られたくないので、
をランダム化した
を集計者に返す。
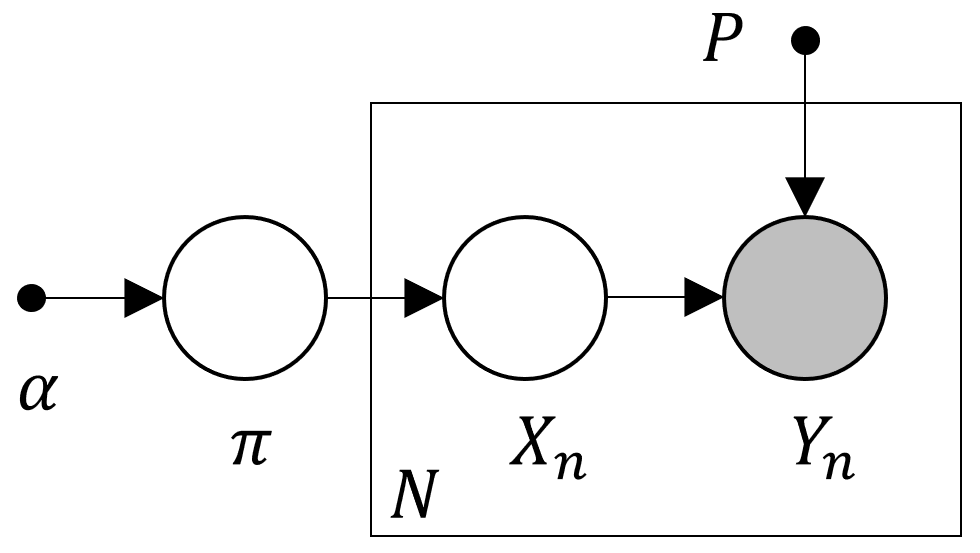
このとき以下のモデルを考える。
ランダム化の確率 からなる計画行列を
と記す。
また にはパラメータ
を持つディリクレ共役事前分布を入れる。
ユーザ の真の回答を
、それをランダム化したものを
で表す。
集計者は 人の回答者のランダム化された回答の観測値
から
などを推定する。
変分ベイズ推論は事後分布に独立性の仮定(変分近似)を入れて、最終的に や
などを計算して更新式を導出する
しかしせっかくなので、より高い性能を期待して LDA(Latent Dirichlet Allocation) でおなじみの Collapsed Variational Bayes を使ってみよう(Teh+2007, Asuncion+2009)。
Collapsed Variational Bayes ではまず変分近似を以下のように弱める。
ただしこれ以降 を
、
を
、
以外の
全体を
で表す。
この仮定に基づき変分自由エネルギー を以下のように展開する。
ここで自由エネルギー を
で最小化する代わりに、まず
で最小化して、次に
で最小化する。
で最小化したものを
と書く。
この を、
に基づいて、各
で反復的に最小化するのが Collapsed Variational Bayes となる。
多項分布となる のパラメータを
とし、
とおくと(ただし
は指示関数)、その更新式は以下のように求められる。
式の最後の近似は、LDA の CVB0 と同じくテイラー展開の 0 次の項のみに近似している。
実験
実装はこちら。
同じ反復法だが、データ件数 でループする必要があるため、Gibbs Sampling より処理が10倍以上重い。そのため、推論の試行とサマリーを分離した上、試行の並列化までしている(苦笑)。
ここまでやっても、 の組み合わせ 9通り×10000試行の推論には手元の環境で10時間かかった。
前回と同様に Randomized Response の計画行列 は1個のパラメータ
で表現し、実験では
を用いる。
個の選択肢を持つ質問に対し、
人のユーザが 1:2:3:4 の割合で回答
、
の Randomized Response でランダム化された回答から推定した
の分布を見る。
事前分布のパラメータによる挙動の違いも見たいので、 を対称なディリクレ事前分布のパラメータとして用いる。
まずは手法ごとの違いを見るため、最尤推定、ギブスサンプリング、そして変分ベイズ(Collapsed Variational Bayes)に対して ごとの推定値の分布を見比べてみる。事前分布のパラメータは
のものを選んでいる。
今回は密度推定した線も書き加えてみたので、分布の形がよりわかりやすい。
| N=100 | N=1000 | N=10000 | |
| MLE |  |
 |
 |
| Gibbs |  |
 |
 |
| VB |  |
 |
 |
最尤推定解は によらず均等な散らばり具合で [0,1] からはみ出すが、ベイズ化によって
を確率値としてモデリングすると解消できることは前回までの記事で見たとおり。変分ベイズももちろんベイズモデルなので、同様に [0,1] に収まるように推定される。
上の図ではギブスサンプリングと変分ベイズの結果はそっくり同じに見えるが、実は縦軸・横軸の数値をよく見ると分かるように、変分ベイズの方が分散が小さい(山も高い)。
それがもっと明確に読み取れるように、 と
について箱ひげ図を書いて、特にそれらの散らばり具合の違いを見比べてみる。
| N=100 | N=1000 | N=10000 |
 |
 |
 |
すべての場合で 変分ベイズ(左) のほうがギブスサンプリング(右) より分散が小さい。横軸の下に書かれた推定値の標準偏差からも、グラフの見た目だけではなく実際に分散が小さくなっていることがわかる。これは推定値の精度が良くなっていることを意味している。*1
次にディリクレ事前分布のハイパーパラメータによる挙動の違いを見る。
ではハイパーパラメータによる差異がほとんどない(データが多いと事前分布の影響が小さくなる)のは前回ギブスサンプリングでも見たとおりなので、
の図を掲載する。
| N=100 | α=0.01 | α=0.1 | α=1.0 |
| Gibbs |  |
 |
 |
| VB |  |
 |
 |
| N=1000 | α=0.01 | α=0.1 | α=1.0 |
| Gibbs |  |
 |
 |
| VB |  |
 |
 |
ギブスサンプリングでは を 1 より小さくすると事前分布の影響が強く出た推定になっていた。特に
の両端が上がった分布(つまり
のどれか1つが 1 で残りが 0)が顕著だろう。*2
それに対し、変分ベイズではそうした極端さはほぼなく、直感に即した真値の周りの山形の分布となっている。
を小さくすることによる平滑化の低減(トレードオフとして分散の増加)を箱ひげ図で確認しよう。平均が理屈通りに振る舞うのは当然なので、今回は中央値に着目してみる。
| α=0.01 | α=0.1 | α=1.0 | |
| N=100 |  |
 |
 |
| N=1000 |  |
 |
 |
まず前回の記事で指摘しそびれていたこととして、ギブスサンプリングの での極端な分布では中央値も真値から大きく離れていることが箱ひげ図から読み取れる。推定値の分散も非常に大きい。
の
では台が [0,1] しかないのに標準偏差が 0.430 と、一様分布(標準偏差 0.289)のほうがマシなレベル。
ギブスサンプリングで のハイパーパラメータを使うのは難しそうだ。
変分ベイズでは、真値の周りの山型分布から想定できるとおり、中央値がちゃんと真値に近い値として推定できている。そして を小さくすると中央値はより真値に近づく。
このように変分ベイズ(Collapsed Variational Bayes)による推論は、最尤推定やギブスサンプリングより良い推定値が得られる。 でも直感的に良い推定値が得られる可能性が十分高く、欲しい精度に合わせてハイパーパラメータを厳選する甲斐がありそう。
実際の観測値に対する推定を行う場合、平均より中央値が外れてないことのほうが嬉しいので(確率 1/2 で中央値以上/以下になる)、その点でも変分ベイズによる推論は筋が良いとわかる。
同じ(真の事後)分布の推定を目的としているギブスサンプリングとの意外なほどの大きな差異が何によって生じているのかは興味深いところ。思い当たる要因は変分近似と CVB0(テーラー展開の0次近似)しかなく、どちらも原理的には精度を下げる効果しかないはずなのに、変分ベイズのほうが自明に良い結果を叩き出すのは、LDA-CVB0 の不思議な性能の良さと同じ根っこにつながっていそう(そう言えば CVB0 の理論的解釈とか誰かやってたような……)。
英語版 (blog articles In English)
References
- Teh, Yee W., David Newman, and Max Welling. A collapsed variational Bayesian inference algorithm for latent Dirichlet allocation. In Advances in Neural Information Processing Systems 19, 2007.
- Asuncion, A., Welling, M., Smyth, P., and Teh, Y. W. On smoothing and inference for topic models. In Proceedings of the International Conference on Uncertainty in Artificial Intelligence, 2009.