Randomized Response はアンケートの回答をランダム化することで、個人の回答は伏せつつ平均などの統計量を得る手法の1つ。
前回記事では、回答の割合の推定量を最尤推定で得る手順を紹介したが、割合の推定値が負になる可能性があることを示した。
shuyo.hatenablog.com
その問題を解消する方法の1つに、統計モデルをベイズ化するアプローチがある。今回はその中でも一番シンプルなギブスサンプリングによる推論を紹介する。
2値アンケートだとベイズ化の効果が見えにくいので、ベイズ化の前にまずは多値化する。
なお、 番目の要素が
であるベクトルを
、
要素が
である行列を
のように簡易的に表記している。
質問 に対する回答者の答えを確率変数
で表す。
回答者は真の回答 を知られたくないので、
をランダム化した
を集計者に返す。
集計者は 人の回答者のランダム化された回答
から
などを推定する。
今 が
通りの回答を持つとし、
ともに
の値を取るとする。
をランダム化した
の確率を
とし
、
を要素とする計画行列
を考える。
のモデルを
としたとき、
の推定値が欲しい回答の割合となる。
の観測値
に対し、過程は省略するが、最尤推定解
は以下のように求められる。ただし
とする。
計画行列 は
個のパラメータを持つが、自由度が多すぎてそのままでは使いにくい。
そこで真値が であるとき、確率
で
、確率
で
から一様乱数で選んだ値を
とするランダム化メカニズムがよく採用される。
この場合、1つのパラメータ に対し、計画行列は以下のように定められる。*1
(式1)
最尤推定解 は 0 から 1 の範囲に収まらないことがある。前回と同様にシミュレーションで確認しておこう。
実験に使ったコードはこちら:
github.com
4個の選択肢を持つ質問に対し、 人のユーザが 1:2:3:4 の割合で回答するとき、ランダム化された回答から
を推定する。
の Randomized Response でランダム化された回答から推定した
をプロットした。



ではいい感じに推定できているが、
では混然一体となってしまっており、
間の大小さえうまく推定できるかどうかわからないことが読み取れる。
Randomized Response のパラメータ を大きくすれば精度は改善できるので、集めたい
の大きさや最低限望む安全性などと相談して
を決める必要がある。
における各
の平均・標準偏差、および 95%信頼区間も見ておこう。
| 0.1 | 0.2 | 0.3 | 0.4 | |
| 0.1 | 0.2 | 0.3 | 0.4 | |
| 0.21 | 0.21 | 0.22 | 0.22 | |
| 95%区間 | -0.3~0.5 | -0.2~0.6 | -0.1~0.75 | 0.0~0.85 |
これほど重なっていても、 はちゃんと成立している。
分散(標準偏差)は によらず一定だ。ここはベイズ版との比較ポイントになるので覚えておこう。
95%信頼区間は思いっきり負の領域にはみだしている。ベイズ化によってこれの改善を図る。
ベイズ版 Randomized Response
に共役事前分布としてディリクレ分布を入れて、その事後分布を推定する。
はディリクレ事前分布のパラメータである。
事後分布の推定には方法はいくつかあるが、ここではまずギブスサンプリングを使った推論を導出しよう。
ユーザ の真の回答を
、それをランダム化したものを
という確率変数で表す。
また 以外の
全体を
で表す。
このとき観測値 に対する事後分布
をギブスサンプリングで求めるのに必要な、潜在変数
および
の全条件付き事後分布を計算する。
(式2)
(式3)
ただし は
の値が
である個数
とする。
はその式の形から
とわかる。
と
の初期値を適当に決めて、(式2) と (式3) からのサンプリングを繰り返せばギブスサンプリングとなる。
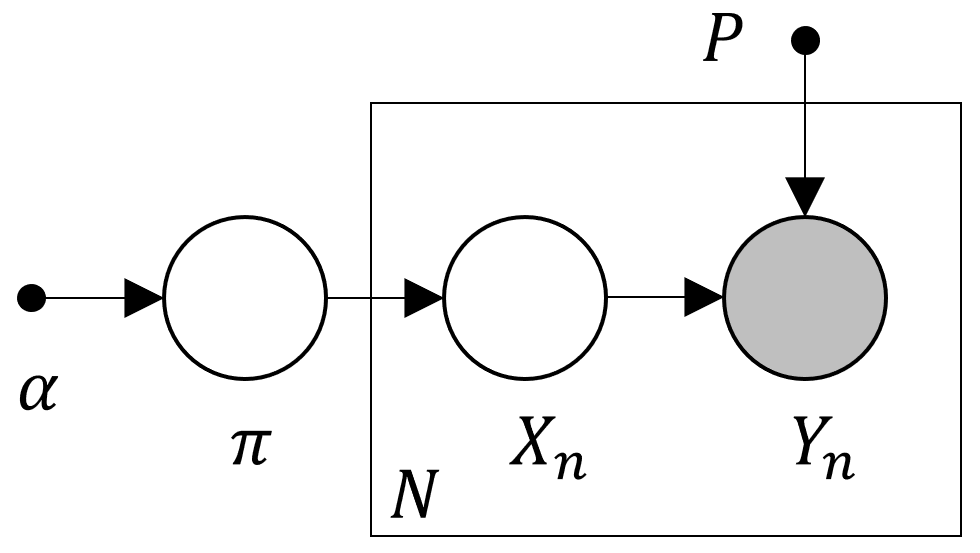
(式2) は、 のサンプリングが他の
に依存しないことを表している。実際グラフィカルモデルを見ると、
を縛れば
は条件付き独立になる。
つまり 全体を一度にサンプリングするようなコードを書くことができる*2。
実験に使ったコードはこちら:
github.com
実装ではサンプリングを400回繰り返し、最初の200回を捨てて、残る 200回のサンプル の系列の平均をとって割合の推定値としている(回数は適当w)。
事前分布のパラメータは と対称とし、まずは
に対してデータの件数
に対して、Randomized Response の試行とギブスサンプリングによる推論を繰り返して得られた分布が以下のようになった。



まず ではきれいな結果になっている。これは問題ないだろう。
が小さくなると分散が大きくなり、最尤推定解が負になることがある問題を解決するためにベイズ化したわけだが、
や 1000 のヒストグラムの横軸を見れば分かる通り、
などの分布もすべて 0 以上の範囲に収まっている。
わかりやすい で見ると、
は左右対称な釣鐘型であるのに対し、
の分布は左の裾が 0 のところにストンと落ちる非対称な分布となっている。
になると分布の重なりは著しくなってしまうが、それでも分布の台が 0 から 1 の範囲に収まることはちゃんと守られている。
この通りベイズ化は期待通りの効果を発揮してくれた様子だが、別の問題も生じている。
における推定値の平均
を見てみよう。
| 0.1 | 0.2 | 0.3 | 0.4 | |
| 0.18 | 0.22 | 0.27 | 0.32 | |
| 0.09 | 0.11 | 0.12 | 0.13 | |
| 95%区間 | 0.06~0.41 | 0.07~0.48 | 0.09~0.54 | 0.11~0.59 |
分散が ごとに異なり、また最尤推定解のそれより小さいなど嬉しいところもあるが、今見てほしいのは最尤推定では成立していた
=\pi_i| が成立しなくなっている点である。
これはディリクレ事前分布によって正則化の効果が生じて、解が平準化されているためだ(0.1,0.2 の推定解は大きく、0.3,0.4 のは小さくなっている)。
ではまたちゃんと
=\pi_i| が成立しており、データが少ないと事前分布に引っ張られるという正しくベイズらしい振る舞いになっている。
では事前分布による正則化の効果を下げるために を小さくしてみたらどうだろう。
それぞれについて事前分布のパラメータを
にしてみたときの推定解の分布が以下の図だ。



では事前分布の違いを感じさせないが、
では
が高い確率で 0 に縮退することがわかる。
における推定値の平均や分散も確認する。
| 0.1 | 0.2 | 0.3 | 0.4 | |
| 0.13 | 0.19 | 0.28 | 0.4 | |
| 0.18 | 0.23 | 0.27 | 0.3 | |
| 95%区間 | 0~0.69 | 0~0.81 | 0~0.89 | 0~0.93 |
を小さくしたことで、たしかに平準化の効果は押さえられ、
は真の割合に近づいている。しかし 95% 区間を見れば分かる通り、一番大きい
でさえも 0 に縮退する可能性が十分ある( PRML に書いてあった「関連度自動決定(ARD)」と同じ効果)。
0 に潰れる可能性があるということは、広い範囲の値を取りうるということで分散も大きくなっている。
このようにベイズ推論を用いる場合は事前分布をうまく決める必要がある、という至極当たり前な結論がでたところで*3、Randomized Response のグラフィカルモデルをもう一度よく見てみると、LDA の簡易版(ドキュメントが1個で、単語の生起確率が given)であることがわかる。
となるとせっかくだから LDA ではポピュラーな Collapsed Variational Bayes 推論も試してみたいよね! ということで次回記事に続く。
Reference
- Oh, Man-Suk. "Bayesian analysis of randomized response models: a Gibbs sampling approach." Journal of the Korean Statistical Society 23.2 (1994): 463-482.