「データ解析のための統計モデリング入門」6.6章割算値はなぜダメなのか？　#みどりぼん

昨日 7/29 の「第6回「データ解析のための統計モデリング入門」読書会」は参加しなかったのだが、ニコ生で中継してくださっていたので後半を聞くことができた。
6.6章「割算値の統計モデリングはやめよう」では、タイトルの通り観測データ同士を割り算するなと話しているわけだが、読んでいていろいろ疑問に思うところがあり。
読書会中継でちょうど 6.6 章以降を担当された 0kayu さんの発表を聞くことができたのだが、気になっていたあたりは特に質疑でも話題にならず残念。
というわけで、誰かがツッコミを入れてくれることを期待して自分の疑問をここに書いておく。

「データ解析のための統計モデリング入門」6.6章では統計モデルに観測データ同士の割り算値を持ち込むことを批判している。その理由として、

比率にすることで元のスカラー値の情報が失われる
値それぞれが分布を持っている場合、それらの割り算値の分布がよくわからない

があげられている。
が、前者は元の値をモデルから除かずに割り算項を加えるだけならいいとも言えるし、後者の理由なら直前の 6.5章で導入した交互作用項（つまり掛け算）もアウトなはずである。
つまり、上の2つではその理由付けには足りていないのではないか（それとも何か誤解してる？）のが疑問の1つ目。

6.6.1 では「ついつい割り算したくなるようなデータ」でも、オフセット項という「わざ」を使えば割り算を回避できるという話を具体例を交えて紹介している（どうしてここで「わざ」という言葉使いをするんだろうという疑問もあるのだが、さすがに枝葉末節かなとも思うので置いておく）。
しかし、紹介されている具体例を見ると、

$\lambda_i=A_i\exp(\beta_1+\beta_2x_i)$

という式で表現されている。これは要するに $\mathbb{E}[y]/A$ をモデリングしているわけだ。
しかしそれと $\mathbb{E}[y/A]$ を比べると、割り算がモデルに入ってしまう後者は「絶対ダメ」と言われてしまうほど本質的に違うものだろうか。

最も大きな違いは、y は整数値(植物個体数)なので、 $\mathbb{E}[y]$ ならポワソン分布でモデル化できるけど、調査地の面積 A で割った $\mathbb{E}[y/A]$ はそういう訳にはいかない、という点にある。
0以上の実数値を扱う分布と言えば真っ先に思い浮かぶ1つはガンマ分布だが、図ったようにみどりぼん 6.8 章はそのガンマ分布を使った GLM の話なわけで、これは試しにやってみろということだろう。

$\mathbb{E}[y/A]=\exp(\beta_1+\beta_2x_i)$

を、y/A がガンマ分布に従うとしてパラメータ推定したのがこちら。

d <- read.csv("http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/binomial/data4b.csv")
(model.poisson <- glm(y~x, offset=log(A),family=poisson,data=d))
(model.gamma <- glm(y/A~x, family=Gamma(link="log"),data=d))

> (model.poisson <- glm(y~x, offset=log(A),family=poisson,data=d))

Call:  glm(formula = y ~ x, family = poisson, data = d, offset = log(A))

Coefficients:
(Intercept)            x
     0.9731       1.0383

Degrees of Freedom: 99 Total (i.e. Null);  98 Residual
Null Deviance:	    261.5
Residual Deviance: 81.61 	AIC: 650.3

> (model.gamma <- glm(y/A~x, family=Gamma(link="log"),data=d))

Call:  glm(formula = y/A ~ x, family = Gamma(link = "log"), data = d)

Coefficients:
(Intercept)            x
     0.9699       1.0516

Degrees of Freedom: 99 Total (i.e. Null);  98 Residual
Null Deviance:	    5.753
Residual Deviance: 1.863 	AIC: 192

上がオフセット項付きポワソン分布、下がガンマ分布。
AIC が出てるとついつい比べたくなるが、それはいくらなんでもダメに決まってる（ヒント：片方だけ連続分布）のでグッと我慢しつつ、推定された係数を見ると非常に近い値が得られている。
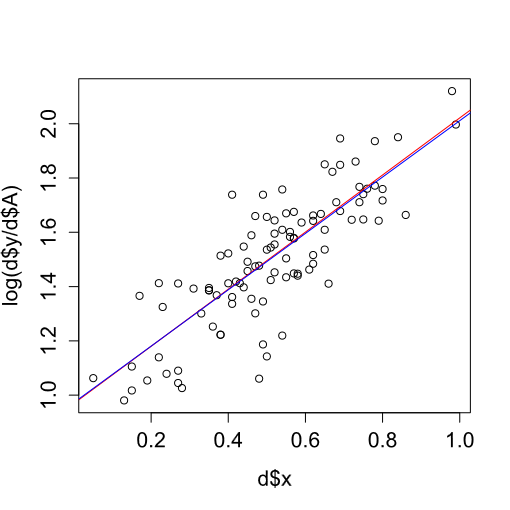
線形予測子をプロットしてみても、ほとんど差がないことがわかる（分布は描くのが面倒なので略）。

plot(d$x,log(d$y/d$A))
abline(model.poisson,col="red")
abline(model.gamma,col="blue")

赤がポワソン、青がガンマ。
「結果だけ」見ると、どちらかがどちらかより確実に良い悪いとは言えなさそう。

みどりぼん p133 には「このようにオフセット項を使うと、個体数平均は調査地の面積 A_i に比例する、といった仮定を反映させつつ明るさ x_i の効果を推定できます。個体数を調査地面積で割って密度にする、といった観測値同士の割り算は全く不要です」とあるが、割り算しないことがまるで目的化しているようにも読めて、個人的にはちょっと気持ち悪い。
ここでポワソンのほうがいいんだろうなと判断する根拠としては、ガンマ分布の方は y が整数値しか取らないことをモデリングできていないからであって、割り算が直接要因ではない、はず。

つまり割り算を避けるべき理由がまだいまいちよくわかってない。
おそらくは割り算値を導入した「全然ダメダメなモデル」をたくさん見てきたことから「割り算ダメ」という経験則が生まれたのだと思うのだが、もうちょっと納得できる理由付けはできるんだろうか、というのが2つ目の疑問。
「割り算を使った特徴を組み込む場合はその妥当性に注意をはらいましょう」くらいの言い方なら特に異論ないのだけど、任意の特徴についても「妥当性に注意をはらいましょう」は言えちゃうので、何も言ってないのに等しいか（苦笑）。

そもそも、「比率にすることで元のスカラー値の情報が失われる」という理由を持ち出すのなら、「割り算したくなる値」が目的変数にあたるこの例は適していない気がする。
そして「割り算したくなる値」が説明変数に来る場合は「オフセットわざ」が使えないのだが、その時はどうするのだろう（それでも割り算はダメ？）、というのが最後の疑問。

【追記】

「データ解析のための統計モデリング入門」6.6章割算値はなぜダメなのか？ #みどりぼん - Mi manca qualche giovedi`? に書いた疑問にコメント・フォローをいただいた。ありがとうございます。

「データ解析のための統計モデリング入門」6.6章割算値はなぜダメなのか？ - URL @shuyoさんから#みどりぼん §6.6 は「なぜ割算値がダメなのか」の説明・例示になってないとのご指摘．たしかに，もっとうまい例示が必要ですね…

2014-07-31 16:08:01 via Twitter Web Client

ぶっちゃけると「割り算はダメ」も「割り算してもいい」も額面通りに信じるつもりはもともとなくて、「○○○○な場合は割り算は筋が悪い」くらいの話なのだろうな、と思っていた。みどりぼんはそこの「限定」がうまく表現できていないのかな、と。

現時点で確実に言えることは、割り算固有の話としては「0やその前後を含む分布が除数に来るような割り算はダメ」という算数レベルの常識くらい。
あとは「ヒストグラムや散布図(R で言う pairs)を描いてみて、これはヤバそうという場合は使わないでおきましょう」という、全ての特徴について言えることを守っておけば、割り算をあえて避ける理由はない（少なくともまだ言語化されていない）という理解で大丈夫そうな雰囲気。