6/10 に開催された「データ解析のための統計モデリング入門」、通称「みどりぼん」の第3回読書会にのこのこ参加& LT してきた。主宰のやまかつさん、発表者&参加者の皆さん、会場を提供してくださったドワンゴさん、ありがとうございました。
LT は……正直、ネタを思いついた時は、ええやんおもしろいやん、とかなぜか思いこんでた。当日の朝くらいに「測度論とかないわー」ということにやっと気づき、一週間前の中谷の後ろ頭をしばき倒したくなったが、もはや後戻りはできず。この LT をちゃんと最後までやり通したという一点で褒めてあげて欲しい……
さて気を取り直して。
質疑応答の時にあれこれ好き勝手なことを突っ込ませていただいてたのだが、読書会終了後にそのあたりをブログとかにまとめてあると嬉しい、という声をもらったので、かんたんにメモしてみる。
3.6 説明変数が数量型+因子型の統計モデル
この節では、体サイズ x と施肥 f の両方を組み込んでポアソン回帰をしてみたら、施肥の係数 β3 が負になっちゃった! という話をする。
しかし、「みどりぼん」はこの教科書的おあつらえ向きな展開にもかかわらず、「前の節(=施肥のみを説明変数とするモデル)では肥料の効果 fT がプラスであったのに、このモデルではマイナスだと推定されています。肥料の効果についてはいよいよわからなくなってきました」とコメントしたのみで終わってしまう。
案の定、読書会ではこの点が議論の的となり、みんなでこの「直感と異なる結果」をどのように解釈するのかを熱く語り合うことになった。このように議論してもらう事を期待して、あえて説明しなかった……?
先に結論めいた事を一言でいうと「説明変数である体サイズと施肥効果の間に、いわゆる弱い相関があるから」となるだろうか。
一般化線形モデルでは説明変数間の独立性をどこか期待している部分があって(「説明変数」「目的変数」ではなく「独立変数」「従属変数」と呼ぶ流儀もあり、このことと関係している……のかな? 由来は調べてない)、そうでない場合はパラメータが「期待する値」から外れたり、精度が悪くなる、などと言われたりする。
といっても、読書会でも指摘のあったことなのだが、「期待する値」とは「説明変数にその変数だけを使って、他の変数の影響を除外した場合の係数」だと解釈することができる。すると、その変数が他の変数と独立なら「期待する値」に一致するだろうし、逆に独立でなければ、その「期待する値」に一致しないのは不思議でもなんでもない。
つまり、パラメータが「期待する値」から外れているように見えて、その「理由」を考察する必要をもし感じたなら、まずは説明変数間の相関を確認するのが一つの手。
そこで体サイズと施肥効果の関係を見てみると、
d <- read.csv("http://hosho.ees.hokudai.ac.jp/~kubo/stat/iwanamibook/fig/poisson/data3a.csv") plot(d$f,d$y) plot(d$f,d$x)
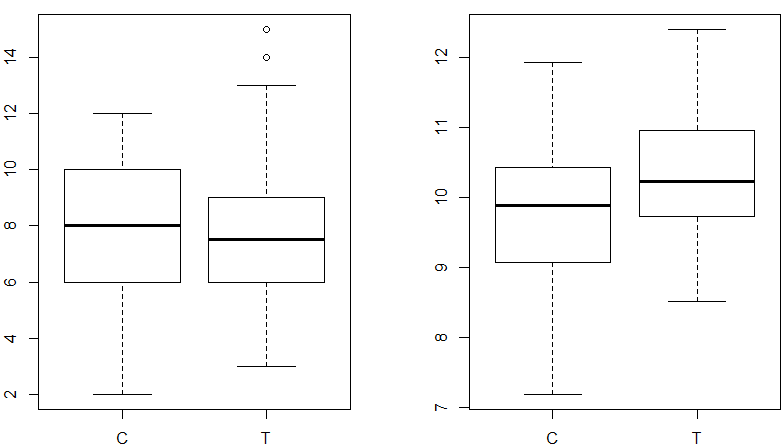
左図が施肥の有無ごとの種子数の関係(みどりぼん図3.3)、右が施肥の有無ごとの体サイズの関係。種子数は施肥の有無と関係なさそうだが、右の体サイズはどうも関係がありそうに見える。
実際 C=0, T=1 として各変数間の相関係数を見てみると(TRUE を 1 、FALSE を 0 とするために +0 している)、
> cor(d$y,(d$f=="T")+0) [1] 0.01914445 # 種子数 と 施肥の有無 > cor(d$x,(d$f=="T")+0) [1] 0.2806593 # 体サイズ と 施肥の有無 > cor(d$x, d$y) [1] 0.2276909 # 体サイズ と 種子数
となり、施肥と種子数は相関がなく、施肥と体サイズ、体サイズと種子数には弱い相関がある、と一般に言われるような相関係数が得られる。
つまり、施肥と種子数の間にも(かろうじて)正の相関があるが、体サイズとの相関で十分説明できてしまっている。したがって施肥による効果は微調整レベル、負になっても不思議はない。そういう解釈をすることもできる。
また、勉強会の質疑で出ていた意見として、「同じ体サイズなら、施肥してそうなったものより、施肥をせずにそうなったもののほうがポテンシャルが高いと考えれば、施肥の係数が負になることは『直感に反しない』」という解釈が納得感が高くておもしろかった。そういう解釈をすることもできる。
一般化線型モデルに限らず統計モデルを現場で使ってみたときの「あるある」ネタとして、得られたパラメータの値、特に正負が「直感と異なる」場合に(上司などから)理由の説明を求められて困る、というのは鉄板の1つだと思うので、「みどりぼん」のような教科書でここらへんフォローしてくれててもいいのに、という気もちょっとする。
そういった時に上のような作文が求められるわけだが、逆にそういう主観的で作為的な作文術に結びついてしまうことを嫌って、この話題を深追いしたくなかったのかもしれない。
ただそういう作文は置いといたとしても、「データ解析で最も重要なのは、まず何はともあれ、そのデータをさまざまな方法で図示してみることです」(p16)とか、「統計モデリングにとりくむときに、そのデータを「いろいろな図にしてよく見る」点は何度でも強調しておきたいところです」(p44)とか、図示の重要性をたびたび強調する「みどりぼん」なら、上で描いた体サイズと施肥の関係を図示しといてほしかったかなあとは思うかな。
あと、p51 で z 値や Pr(>|z|) といった指標の説明をしておきつつ、施肥を説明変数に加えてパラメータの効果が「いよいよわからなくなってきました」というとき、なぜこのモデルでの z 値などを示さなかったのかも疑問。まあモデルの選択は次の章の AIC に全て託した、ということなのかなあ。
ちなみに z 値類を出してみるとこんな感じ。
> fit <- glm(y~x+f, data=d, family=poisson)
> summary(fit)
Call:
glm(formula = y ~ x + f, family = poisson, data = d)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.3977 -0.7337 -0.2023 0.6795 2.4317
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.26311 0.36963 3.417 0.000633 ***
x 0.08007 0.03704 2.162 0.030620 *
fT -0.03200 0.07438 -0.430 0.667035
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 89.507 on 99 degrees of freedom
Residual deviance: 84.808 on 97 degrees of freedom
AIC: 476.59
Number of Fisher Scoring iterations: 4fT の z 値は -0.430 ( 0 から十分離れていれば有効なパラメータ)、Pr(>|z|) は 0.667035 ( 0 に近いほど有効なパラメータ)ということなので、fT は有効なパラメータとはなさそうだ、ということが3章の知識からだけでも推測できる、と言っていいのかな?
ちなみに AIC は、上の summary にも出てるが 476.59。
施肥を加えなかった場合の AIC は、
> fit <- glm(y~x, data=d, family=poisson) > summary(fit) (中略) AIC: 474.77
なので、こちらからも施肥を加えない方がいい、という結論に。