2016-04-01

コサイン類似度が高いベクトルはどれくらい似ているか(岩波データサイエンス刊行イベントより)

岩波データサイエンス vol.2 の発刊を記念して、刊行トークイベント「統計的自然言語処理 - ことばを扱う機械」が 3月3日に開催されました。

イベントの様子はニコニコ動画さんで生中継されましたが、その録画は YouTube で公開させてもらっています。

【トークイベント「統計的自然言語処理ーことばを扱う機械」（岩波データサイエンス Vol.2 刊行記念） - YouTube】

自然言語処理に詳しい人でも詳しくない人でもおもしろい本＆イベントになったので、ぜひ一度手にとって見てもらえると嬉しいです。
よくわからないけどちょっと味見してみようかなという人には、賀沢さんの招待講演がユーモアたっぷりですので、まずはそれを笑って楽しんでみては。

以上、1ヶ月遅れ(刊行からは2ヶ月遅れ……)の宣伝終わり。

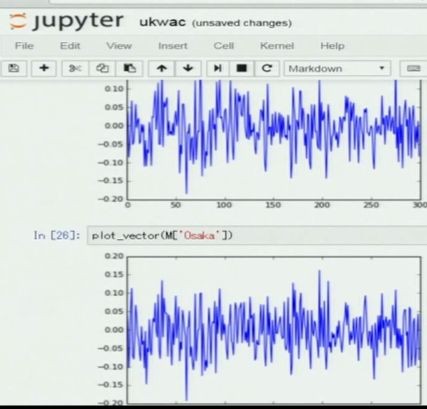
さて、上記イベントで東北大の岡崎先生が、ご発表の冒頭で word2vec で "Tokyo" と "Osaka" のベクトルが似てるという話をしてくださった。

岡崎先生の発表(19分23秒から)

word2vec によって学習した300次元のベクトルそれぞれをplotして、
「結構似てませんか」
「びっくりしたんですけど、視覚で見ても結構似てるなとわかる」
「このくらいの(コサイン)類似度(0.84)だと視覚的に見てもわかるんだな」

（岡崎先生の発表動画より）

とやらかす(失礼)と、会場はドッと受けていたわけだが、実際見た目よく似てる(よね？)。

まあ「見た感じ似てる」とかいうのは主観的過ぎるし、人間の習性的にどうしても「違い」に目が行ってしまうかもしれないが、ピークの位置と大きさはほぼ重なっており、少なくともコサイン類似度が高いことには納得できるのではないだろうか。

そう言われてみて遅まきながら気づいたのだが、高次元でコサイン類似度が大きいというのは、実は「めちゃめちゃ似ている」んじゃあないだろうか。
言語処理っぽいことをしてれば、コサイン類似度をクラスタリングとか判別とかに使うわけで、そのとき 0.6 くらいの値しか出ないと、なんか小さいなあとか思っちゃってたけど、 0.6 くらいでも実は「結構かなり似ている」んじゃあないだろうか。

ランダムな2つのベクトルのコサイン類似度はどういう分布になるのだろう。

まず2次元空間で考える。
2次元球の周囲(つまり円)の上で、とりあえず適当なしきい値としてコサイン類似度が 1/2 以上になるのは、それはあるベクトルの±60度の中にもう1つのベクトルが入る場合である。
よって、コサイン類似度>1/2 となる確率は 1/3 だ。

3次元空間だと、3次元球の表面上を考えて、(cosθ>=1/2な面積) / (球の面積) でその確率は 1/4、と少し減る。

4次元以上の一般の n 次元空間でその確率を求めるには一般の n 次元球の表面積(の一部)を計算する必要がある。
ちょっと考えてみたが、めんどくさい方法しか思いつかなかったので、サンプリングで解かせることにした。
1000000 サンプルのうちコサイン類似度が 1/2 を超える割合を求めると、

10 次元では 0.06 (約 1/17)、
20 次元では 0.01 (約 1/100)、
30 次元では 0.0021 (約 1/480)、
40 次元では 0.00042 (約 1/2400)

と、どんどん少なくなっていき、100 次元では、1000000個サンプリングした中にコサイン類似度が 1/2 以上になる点はなかった。

こうしてみると、300次元でコサイン類似度が 0.84 とか、もしそれがランダムに取ったベクトルだったなら、宝くじに当たるとか言うレベルの話ではないくらい珍しい現象であることがわかる。

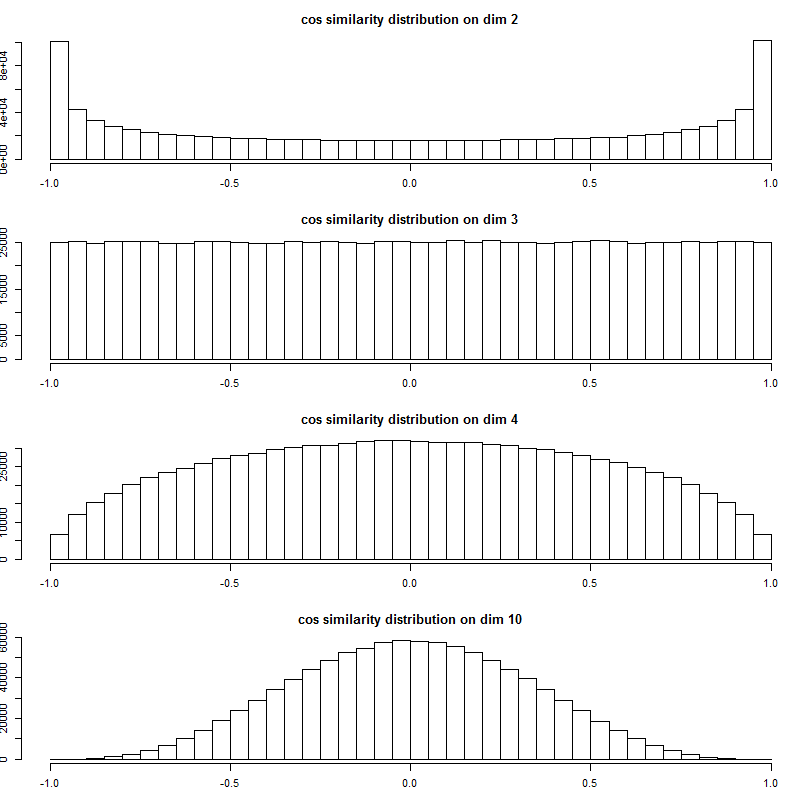
コサイン類似度の分布も見てみよう。
上から 2次元、3次元、4次元、10次元、20次元、30次元、40次元、100次元だ。

2次元ではむしろ ±1 の周辺に多く分布しているのが、高次元になればなるほど、ランダムな2つのベクトルのコサイン類似度は 0 の近辺に大きく偏って集中していくことがよくわかる。
300次元の世界では、適当に取った2つのベクトルはほぼ直交している！

人間は2次元3次元までしか直接的には知覚できないので、どうしても2次元3次元あたりの感覚をそのまま高次元にも当てはめてしまいがちだが(次元の呪いの正体)、この分布を見るとコサイン類似度についてもその感覚が非常に危険であることがよく分かる。
今度からコサイン類似度で 0.6 とかいう値になっても「0.6 しかない」ではなく「0.6 もある！」と思うようにしよう。

岩波データサイエンス Vol.2

作者: 岩波データサイエンス刊行委員会
出版社/メーカー: 岩波書店
発売日: 2016/02/17
メディア: 単行本（ソフトカバー）
この商品を含むブログ (3件) を見る

2016-02-03

「続・わかりやすいパターン認識」13章「共クラスタリング」の無限関係モデル(IRM)の数式について #ぞくパタ

ぞくパタノンパラベイズクラスタリング

続わかりやすいパターン認識、 6章から読み始めたんだけど（ぉぃ）、いきなり式 (6.9) が間違ってた。簡単なミスなので既知だと思うんだけど、正誤表ってどこかにないのかなあ。#ぞくパタ
— Nakatani Shuyo (@shuyo) March 10, 2015

ということを1年近く前につぶやいたりしてたのだが、オーム社のサイトで「続・わかりやすいパターン認識」(以降「ぞくパタ」)の正誤表がちゃんと公開されていることに最近ようやく気づいた。

続・わかりやすい　パターン認識 −教師なし学習入門−｜正誤情報等のご案内｜Ohmsha

上のツイートで言っている式 (6.9) ももちろん修正されているし、以下の記事で書いていた8章の問題点もことごとく手当されている。すばらしす。

「続・わかりやすいパターン認識」の8章「隠れマルコフモデル」の問題点 2つ #ぞくパタ - 木曜不足

まあこのツイートやらブログやらを参考にしてもらえたかどうかは定かではないわけだが、どこかで間違いを指摘しておくと反映される可能性がある、というのは勇気づけられる話。

話は変わって、2014/12 から開催されていた「続・わかりやすいパターン認識」読書会が先月めでたく最終回を迎えた、っぽい。

第15回「続・わかりやすいパターン認識」読書会 - connpass

「ぽい」というのは、最後の2回に参加できなかったから。
まあもともと興味のある回にとびとびにしか参加してなかったわけだが、12章後半はある意味ディリクレ過程混合モデルの実装編で、この本のクライマックスだったから是非参加したかった。13章の無限関係モデル(IRM)も一応参加してみたかったところ。

というわけで参加できなかったフォローというか腹いせというか、で無限関係モデルを実装でもしてやろうと思って本を読み始めたのだが……。

まだ読んでいる人が少ないせいだろうか、少なくない数式が結構大胆に間違っている。
まあ、だいたいどの間違いも一目見て間違っていることはわかる(左辺に j がないのに、右辺に消えない j が残っている、とか)ので、抜き打ちの演習みたいなものか。
「これくらい計算できるよね？」という読者への親心を無下にするのも心苦しいが、見つけてしまった間違いはじゃんじゃん指摘してしまおう。

というわけで、この記事はぞくパタ13章の数式の誤りを淡々と指摘するだけの記事であり、IRM(Infinite Relational Model) がなにかわかるような記事ではないので、あらかじめ。

まずは p284 の式 (13.8)。右辺の分母に n が現れているが、実は n なんてどこにも定義されていない。
$n_i^1$ とか $n_{(k,+)(i,j)}$ とか、そういうややこしいのはいろいろ定義されている*1からだまされるかもしれないが、ワナである。
この n の位置に入るのは、 $s_k^1$ の個数なので正しくは K である。

$P(s_k^1=\omega_i^1|{\boldsymbol s}_{-k}^1)=\begin{cases}\frac{n_i^1}{K-1+\alpha}\hspace{3ex}&(\text{existing cluster})\\\frac{\alpha}{K-1+\alpha} & (\text{new cluster})\end{cases}$

次は同じ p284 (13.9) 式の新規クラスタのときの式。 $G_0({\bf\theta}_{i,+})$ という記号が出てくる。
11章12章でさんざん見てきたので、ついうっかり知ってる記号だと思ってしまったかもしれないが、これも未定義である。
G_0 は11章12章ではディリクレ過程の基底分布として使われていた記号だが、13章では2次元の構造を持つクラスタを素のディリクレ過程ではモデリングできず、CRP(中華料理店過程)でモデリングされているため、そもそもディリクレ過程自体が出てこない。

「ディリクレ過程だったら基底分布にあたるもの」なら p281-282 にて導入されているベータ分布が相当する。
では G_0 はベータ分布なのだろうと解釈すると (13.9) 式で困ったことになる。

$G_0(\theta)={\rm Be}(\theta;a,b)$

G_0 はパラメータθ(スカラー)の分布であり、それを束ねた ${\bf\theta}_{i,+}$ (ベクトル)の分布ではないので、 $G_0({\bf\theta}_{i,+})$ という書き方は厳密には間違いとなる。
と、なんかややこしげに書いてしまったが、解決方法は簡単。G_0 じゃなくて単に $P({\bf\theta}_{i,+})$ と書いて同時分布にしてしまえばいい。厳密に考えても何の問題もなく、当たり障りもない。いや、この本の表記だと小文字 p か。

次、p287 (13.26) 式。左辺に j がないのに、右辺に消えない j が残る。
これは \prod 忘れなので、単純に正解を記そう。(13.9) 式と同じく未定義 n も手当すると、場合分けの式それぞれ次のようになる。

$\displaystyle\frac{n_i^1}{K-1+\alpha}\prod_j\frac{B\left(n_{(+,+)(i,j)}+a,\;\tilde{n}_{(+,+)(i,j)}+b\right)}{B\left(n_{(-k,+)(i,j)}+a,\;\tilde{n}_{(-k,+)(i,j)}+b\right)}$

$\displaystyle\frac{\alpha}{K-1+\alpha}\prod_j\frac{B\left(n_{(k,+)(i,j)}+a,\;\tilde{n}_{(k,+)(i,j)}+b\right)}{B(a,\;b)}$

(13.27) 式も同様なので、略。ただし、n は L になる。
もっとも、K-1+α も L-1+α も k や l に依存せず、どうせ全部足して1にするときに消えてしまうから、どちらにせよ実装では省略してしまってよかったりする(笑)。

最後、p288 (13.28)式。 k,l が消えずに残る。これも \prod 忘れ。
例によって未定義 G_0 があるので、これも $p(\theta_{ij})$ と直してあげつつ、2行目の式だけ正しく書きなおすとこうなる。

$\displaystyle =P({\bf s}^1)P({\bf s}^2)\prod_{i=1}^{c^1}\prod_{j=1}^{c^2}\int\prod_{k:s_k^1=\omega_i^1\\l:s_l^2=\omega_j^2}P(R_{kl}|\theta_{ij})p(\theta_{ij})d\theta_{ij}$

見つけた間違いはこれで打ち止めだが、2点蛇足。

その1。
この本の積分はちゃんと閉じた形式に計算しつくされており、実装者は自分で計算する必要がほとんどなくてすばらしいのだが、本文最後の積分であるこの $\int\prod_{k:s_k^1=\omega_i^1\\l:s_l^2=\omega_j^2}P(R_{kl}|\theta_{ij})p(\theta_{ij})d\theta_{ij}$ だけは計算されていない。
ここまでの計算が全部できていたらこれくらい朝飯前(誇張抜き)なので、例によって抜き打ち演習として残しておいてもいいんだけど、せっかく全部の積分がやっつけられているのに雑魚一匹だけ残しておくのもなんだよなあ。というわけで、計算してしまおう。

$\int\prod_{k:s_k^1=\omega_i^1\\l:s_l^2=\omega_j^2}P(R_{kl}|\theta_{ij})p(\theta_{ij})d\theta_{ij}=\frac{B\left(n_{(+,+)(i,j)}+a,\;\tilde{n}_{(+,+)(i,j)}+b\right)}{B(a,\;b)}$

その2。
p288 に「P(s^1), P(s^2) は式 (11.11) のイーウェンスの抽出公式で求める」とある。そういえば 12章でもほぼ同じ文言を見た(p265)。
というわけで式 (11.11)「だけ」で P(s) 類が計算できる……と思ったらこれがワナだったりする。

式(11.11)をよく見てみよう。

$P_E(n_1,\cdots,n_c)=\cdots$

左辺は P(s) ではなく $P(n_1,\cdots,n_c)$ なのである。実は、P(s) は並べ替えの自由度の分、確率はこれより下がる。
心配しなくても大丈夫、P(s) と $P(n_1,\cdots,n_c)$ の変換式は式 (11.17) としてちゃんと載っている。
というわけで「P(s^1), P(s^2) は式 (11.11) のイーウェンスの抽出公式と式 (11.17) で求める」だと親切である。

と、あれこれ書いたが、当然、ここに書いてあることにも誤りが含まれている可能性はある。もし間違いなどあればご指摘歓迎。
IRM 実装編はまた今度。

【追記】
社内勉強会の資料公開した。

無限関係モデル (続・わかりやすいパターン認識 13章): https://www.slideshare.net/shuyo/infinite-relational-model

【／追記】

*1: $n_i^1$ と $n_{(k,+)(i,j)}$ では数えている対象が異なるので、個人的にはどちらかは m とか記号を変えて欲しかった。

2015-10-26

EMNLP 2015 読み会 #emnlpyomi

勉強会自然言語処理

10/24 に開催された EMNLP 2015 読み会にのこのこ行ってきた。
主宰の @unnonouno さん、参加者＆発表者の皆さん、会場提供してくださったリクルートテクノロジーズさん、おつかれさまでした＆ありがとうございました。

EMNLP2015読み会

Proceedings を見たら、まあ見事に word embeddings だらけ！　ちゅうことは読み会は word embeddings 祭りやな！　と思ってたら、みんなもそう読んで避けたのか、Proceedings の印象よりだいぶ word embeddings 率が低かった（定量的に確認はしてない）。

ただ、メインはまったく別のモデルでも、特徴量として word embeddings（というか word2vec）を組み込むというのはなんかデフォルトみたいになってきてる気がする。自分が読んだ Topic Model のやつもそうだったし。
休憩時間にもそこらへん話題になり、「使ってなかったら、なんで使ってないのか質疑で突っ込まれるから、使わないわけにいかない説」が出て、うなずけてしまうくらい。
tf-idf みたいな、定番の特徴量として定着するんだろうかなあ。

以下、発表の短い感想（あくまで感想）。読み会資料が公開されているものはそれも。

It’s All Fun and Games until Someone Annotates: Video Games with a Purpose for Linguistic Annotation (@tootles564 さん)

元論文

ゲーミフィケーションでアノテーションする話。
スマホになって、かえってレトロやチープなゲームが受けてたりもするから、ありっちゃありと思うけど。
無理にゲーミフィケーションするから、アノテーションをゲームの文脈に組み込まないといけなくなって、結局ゲームもアノテーションも両方破綻しているような気がしないでもない。
reCAPTCHA のように「アノテーションの報酬としてゲームができる」（広告代わり）とか、スプラトゥーンのマッチング待ちの間に遊ぶミニゲーム（イカジャンプ）のように、ちょっとした合間に出てくるので暇つぶし感覚でついついアノテーションしてしまう、っていうのでいいんじゃあないかなあ。ゲームの文脈からも切り離せるし。

Learning Better Embeddings for Rare Words Using Distributional Representations (@Quasi_quant2010 さん)

Learning Better Embeddingsfor Rare Words Using Distributional Representations from Takanori Nakai

Skip-Gram が流行ってるけど、レアワードの特徴を捉えるには CBOW の方がよくて、うまく混ぜるとよりいい感じになる話。
質疑でも懸念されてた「コーパスサイズによって閾値を変える必要があるんでないの？」あたりはあるとしても、理屈は納得感高い。

A Graph-based Readability Assessment Method using Word Coupling (@niam さん)

EMNLP 2015 yomikai from Yo Ehara

ラベル伝搬で文の難易度を当てるタスクを解く話。
Readablity は、ずいぶんまえだけど少し興味あって調べてたりしてた（といっても機械学習的な手法ではなく、この論文の baseline にも登場している Flesch-Kincaid などのルールなアプローチくらいまでしか手出してないけど）。
途中の行列積のところ、もうちょっと書き下せば意味がわかるようにできる気がしないでもないんだけどなあ。

Long Short-Term Memory Neural Networks for Chinese Word Segmentation (@MasakiRikitoku さん)

中国語の分かち書きがすげー難しそうな例文を正しく分かち書きするには、その文自身をトレーニングデータに含めるしか無さそうな気もするんだがどうだろう。
LSTM(RNN)と系列ラベリングを組み合わせる枠組みは、他の問題にも普通に適用できそうな雰囲気があるけど、すでにポピュラーなアプローチだったりするのかな。

Compact, Efficient and Unlimited Capacity: Language Modeling with Compressed Suffix Trees (@jnishi さん)

Emnlp読み会資料 from Jiro Nishitoba

Compressed Suffix Tree を使って、∞グラムを高速かつ省スペースで構築する話。
道具立ては非常にシンプルなので、なんか初出なの？　感が。
Kneser-Ney でいくら頑張って interpolate しても、一般的なコーパスサイズでは 6 or 7-gram あたりで perplexity は頭打ち、という実感が裏付けられてよかった（小並感）。

Evaluation methods for unsupervised word embeddings (@nozawa0301 さん)

Evaluation methods for unsupervised word embeddings EMNLP2015 読み会 from nzw Nozawa

word embeddings いっぱいあるんで比べてみました話。
順位相関で評価したのと Amazon MTurk で評価したのが一致するってのはちょっと嬉しいかも。
最後の方の議論のところは、なにかおもしろそうなことを言っている予感はあるのだけど、ピンとこなかった。元論文読むか。

Effective Approaches to Attention-based Neural Machine Translation (@tkng さん)

エンコーダー/デコーダーモデル＋Attention に、さらに local attention なるものを組み込む話。
パッと見、劇的な効果がある雰囲気はない。
エンコーダー/デコーダーモデルで固有名詞が入れ替わってしまうのを抑えられるので十分嬉しいということなのかな。

Humor Recognition and Humor Anchor Extraction (@yag_ays さん)

Humor Recognition and Humor Anchor Extraction from yag ays

ユーモア文かそうでないか判定する話。
韻とかいろいろな特徴量を設計して頑張って分類器作るんだけど、baseline の word2vec がそこそこいい性能さくっと叩き出していて、そら word embeddings 流行るわー、という気分に。
そういえば、なぞかけ生成やってはる人いたなあ。

Efficient Methods for Incorporating Knowledge into Topic Models ( @shuyo )

[Yang, Downey and Boyd-Graber 2015] Efficient Methods for Incorporating Knowledge into Topic Models from Shuyo Nakatani

大規模トピックでも効率よく学習するのが歌い文句の SparseLDA （Yao+ 2009, モデルとしては生 LDA と等価）に、事前知識を組み込む話。
いつも読み会に参加するときは、10本くらいの論文の中からある程度読み込んでから選ぶのだけど、今回は余裕なくてイントロとモデルを斜め読みしたくらいで選んだら、

アカデミックの論文はたかだか 1000トピックだが、最近の実用アプリケーションは 100万トピック！　とイントロでぶちあげながら、提案手法は事前知識組み込みで遅くなっちゃって、500トピックで評価
評価指標に使った Coherence は、事前知識を制約に入れた Dirichlet Forest-LDA などより生 LDA の方が良い数値。その状態で「提案手法は LDA を上回っている（ただし僅差）」って言われても、その指標を評価に使うのが間違っているとしか思えない

というわけで、選ぶならせめて評価は読まないと、という教訓。
これがもし読み会トリだったら、ものすごいビミョウな空気で終わることになってしまってたので、そうじゃなくて本当に良かった。

A Neural Attention Model for Abstractive Sentence Summarization (@kiyukuta さん)

A Neural Attention Model for Sentence Summarization [Rush+2015] from Yuta Kikuchi

Attention で文要約する話。
Attention ってソフトなアライメントだよね、って言われて聞くと、なるほどいろんな応用先がありそうだなあという気にさせられる。

2015-09-14

「調査観察データの統計科学」読書会資料を公開しました（数式周りをフォロー）

傾向スコア因果効果

因果推論、特に傾向スコアについて日本語で学ぼうとしたら、第一に名前が挙がるのは「調査観察データの統計科学」だろう。

調査観察データの統計科学―因果推論・選択バイアス・データ融合 (シリーズ確率と情報の科学)

作者: 星野崇宏
出版社/メーカー: 岩波書店
発売日: 2009/07/29
メディア: 単行本
購入: 29人クリック: 285回
この商品を含むブログ (26件) を見る

ところがこの本、数式を中心に難が多く、読み始めたはいいけど困っているという人がかなり多そうだ。実は社内の機械学習勉強会でこの本を紹介したのだが、数式のフォローがかなり大変で、そこそこ端折ったにもかかわらず、３章が終わるまでに７回ほどかかってしまった。
特に３章頭の「難所」については、社内勉強会の時の資料をもとにメモを書いてブログに公開したりもしている。

ひと段落したら勉強会の資料も公開しようかと思っていたのだが、３章をとりあえず終わらせたところで力尽きて、ほったらかしにしてしまっていた（忘れていたともいう……）。が、上の記事のコメントで公開要請をいただいたので、ようやく重い腰を上げて資料を整え公開した。

星野「調査観察データの統計科学」第1＆2章 from Shuyo Nakatani

星野「調査観察データの統計科学」第3章 from Shuyo Nakatani

１・２章についてはおそらく大きな問題はない。せいぜい、層別解析の紹介がおざなりすぎることくらいだろう（それは他の本で得るべき知識というスタンスなのだと思う）。
３章は、つじつまの合わない数式や記述が正直かなり多い。スライドではできる範囲でフォローしたつもりだがもちろん完全ではない。因果推論が専門なわけでもなんでもないので、「こうならつじつまがあう」という想像に基づくフォロー自体が適切ではない部分だってきっとあるだろう。資料の間違いや勇み足については指摘大歓迎なので、ぜひ。

書籍と対照させながら読んでもらうためのものなので、原則として記号は書籍のものを踏襲している。が、ひとつだけ記号の付け替えを行っている(θの真値をθ_0 から θ^* に)。
理由はスライドの中でも説明しているし、実際に数式を追ってもらったら納得いくと思うが、念のため。

企業で取り扱うデータの多くは、この本で言う「調査観察データ」、つまり実験室的セッティングが許されない状況で集められたデータであり、そんな「調査観察データ」でもバイアスを抑えた分析ができる（かもしれない）傾向スコアは多くの人が興味を持つ可能性があるだろう。
それなのに、数式が追えないという理由だけで詰まったり読まれなかったりするのはもったいない。この資料が「調査観察データの統計科学」を読む人の助けになれば幸いである。

え？　４章以降はって？　まだ読んでないっす……。た、たぶん４章以降は３章ほど大変じゃないと思うよ。きっと……。

2015-07-15

「続・わかりやすいパターン認識」11章「ノンパラメトリックベイズ」の「クラスタリングの事前確率」について

ぞくパタノンパラベイズ

昨日の「続・わかりやすいパターン認識」読書会にて、「ホップの壺や中華料理店過程のシミュレーションをみると、これを使うと均等にクラスタリングされるのではなく、クラスタサイズが大きいものから順に小さくなっていくようなクラスタリングがされるように見えるのだが、その認識で正しいのか」といった感じの質疑があった。
いい質問。

実は「続・わかりやすいパターン認識」(以降「ぞくパタ」)では、 p225 の「クラスタリングの事前確率の考え方」のところに、ダイレクトにではないがその質問の答えにつながることが書いてあったりする。coffee break というコラムの形になっているので、つい読み飛ばしちゃった人も多いかもしれないが、結構大事なことが書いてあるので一度じっくり読んでみるといい。

そのあたりも含めて読書会でフォローした内容をここにメモしておく。

まずそもそもの話として。
ベイズにおいて、事前確率（事前分布）の選び方に論理的な裏付けがありうるのか、というと、実のところ全く何もない。ぶっちゃけ事前分布はなんでもいい。
手前味噌だが、そのあたりのことは gihyo.jp での機械学習連載で書いたので、興味があれば一度。

第10回ベイズ確率：機械学習はじめよう｜gihyo.jp … 技術評論社

理論的にはなんでもいいが、そこに人間様の都合が絡むと、こういう事前分布は困る、とか、こういうのは嬉しい、とか出てくる。
望ましい事前分布の条件として、どんな問題でも共通して求められるとすればこの 2つだろう。

ありうる事象（今回の場合は分割方法）の確率が非ゼロ
なんらかの方法で事後分布が計算できる

共役事前分布は後者の「計算できる」を最優先にした選び方になる。共役でなくても、今回のディリクレ過程のように「ギブスサンプリングできる」でもいい。そこらへんの詳細は 12章でやる話なので、ここではとりあげない。

ベイズ公式を見ればわかるが、事前確率がゼロである事象は、たとえどんなデータをもってきても、事後確率もゼロである。よって「ありうる事象」、つまり「答えとして考えられるすべての可能性」には非ゼロの確率を与えておかないといけない。
今やりたいことは「クラスタ数をあらかじめ決めない」なので、クラスタ数が3個でも4個でも5個でも、何個であってもちゃんと非ゼロの確率を持つ事前分布が必要なわけである。

さて、これで冒頭の質問に答える準備ができた。
ここで大事なことは、事前確率は非ゼロでさえあればどんなに小さくても（理論的には）いいということ。
ホップの壺（中華料理店過程）は、色（テーブル）ごとの玉（客）数の偏りが大きい分布だが、均等な分割、たとえば 500個の玉について 100, 100, 100, 100, 100 という割り方にもちゃんと非ゼロの確率が割り振られる。現実には到底観測されることなんかあり得ないほど低い確率だろうけど、ゼロでさえなければ、データが何とかしてくれる期待が持てるわけだ。

ただし、いくら何でもいいといっても、事前分布が「変」であるほど、「正しい答え」にたどり着くには膨大なデータ数が必要になる。逆に言えば、データ数が少ないと事前分布に引きずられる。
例えば 3 クラス× 50 データの iris データセットを 12章のディリクレ過程混合モデルに食わせると、100, 50 の2個のクラスタにまでは分かれるのだが、そこから分割が進まなかったりする*1。k-means （もちろん3クラス決め打ち）などなら、50, 50, 50 に近いところまで行くのだが。
これはおそらく事前分布であるディリクレ過程に引きずられているのだろう。

というわけで冒頭の疑問の答えは、均等な分割もちゃんと行われうるから大丈夫！　という点では No だが、事前分布に負けて、希望よりも偏ったクラスタになることもあるという点では Yes でもある。
それなら、中華料理店過程のような偏った分割モデルではなく、もっと一様な分割を考えたらいいのでは？　という発想が当然出てくるだろうが、実は可算無限な台を持つ一様分布は作れない（ちょっと考えれば雰囲気はわかる、はず）のと同じ理由で、どうしたって傾斜を持たせるしかなかったりする。

つまり、ディリクレ過程（やホップの壺や中華料理店過程）は、上の「任意クラスタ数で非ゼロ＆計算できる」という条件を満たす中で一番易しいものなのだ。
とはいえ、他にもノンパラメトリックベイズのための無限分割モデルは解きたい問題にあわせて考えられており、ぞくパタ 11.4 でちらっと紹介されているピットマン・ヨー過程*2はその代表的な一つである。

読書会では、ピットマン・ヨー過程がなぜかついでに紹介されているっぽい刺身のツマのような扱いを受けていて、あわてて言語処理ではめっちゃ重要ですから！　と突っ込んだり（笑）。
ある分野でどんなに有名であっても、その隣接分野ですら知られているとは限らないというよくある現象なんだけどね。

*1:ぞくパタに書かれている「全パターンが 1 つのクラスタに所属」という初期化だと、実はそれすらもままならず、150個が 1 クラスタのままから動かなかったりする

*2:ぞくパタで「ピットマン・ヨー過程」だといって紹介されているのは、正確には「中華料理店過程をピットマン・ヨー過程に対応するように拡張したもの」ではあるが

2015-07-14

中華料理店過程のテーブル数の分布が見てみたい・実験編 #ぞくパタ

ぞくパタノンパラベイズ

今日のぞくパタ読書会の予習に「続・わかりやすいパターン認識」(以降「ぞくパタ」)の 11章をつらつら読む。
p227 に「CRP における使用テーブル数の変化」というグラフがあり、αが 2 と 10 のそれぞれにおいて、来客数が 1000 になるまでシミュレーションしたときのテーブル数の推移が示されているのだが、当然ながら一回の試行しか描かれていない。
中華料理店過程(CRP)ないしホップの壺をちょっこり試すだけなら 10行ちょっとのスクリプトでできる話であり、実際やってみると、実行するたびにテーブルの増え方が結構変わる。つまり一回の試行ではぶっちゃけよくわからん。

というわけで、α=2 について 1000 回シミュレーションを行い、来客数がそれぞれ 100, 200, 400, 600, 800, 1000 になったときのテーブル数の分布を箱ひげで描いてみた。

ほとんどは中心の周辺にきれいにまとまるけど、散らばりもそれなりにある。
また、テーブル数がある程度増えた以降は、分散はほとんど増えなくなっていく（散らばり具合は n が少ないうちにだいたい決まっちゃう）ということもわかる。テーブルの増える確率がどんどん小さくなることから想像できる通りではあるが。

ちなみに、それぞれの平均値と標準偏差はこんな感じだった。

100: mean=8.31(8.39) sd=2.47(2.42)
200: mean=9.69(9.77) sd=2.78(2.68)
400: mean=11.03(11.14) sd=3.07(2.93)
600: mean=11.86(11.95) sd=3.20(3.06)
800: mean=12.41(12.53) sd=3.25(3.15)
1000: mean=12.88(12.97) sd=3.27(3.22)

カッコ内はそれぞれの理論値。1000 サンプルにしては悪くない？
平均値(期待値)は前回の記事「ディリクレ過程(中華料理店過程)のトピック数(テーブル数)の期待値を導出してみる #ぞくパタ - Mi manca qualche giovedi`?」で求めていたが、分散も「独立な確率変数の和の分散は、分散の和」*1であることに注意すればまったく同様に求めることができる。

ここでは厳密さが欲しかったわけじゃないのでシミュレーションでお茶を濁したけど、実は二手間くらいかければ確率質量関数も計算できる。もし知りたかったら「ポアソン二項分布」で検索。

大したものではないが、シミュレーションのスクリプトも一応貼っておく。
中華料理店過程は、事後分布とか絡まなければ、実装はとても易しく楽しいので、興味あればこんなん見ないで自分で実装してみる方がいい。

import numpy

alpha = 2.0

labels = [100, 200, 400, 600, 800, 1000]
target = dict()
data = []
for i, x in enumerate(labels):
    target[x] = i
    data.append([])

for i in xrange(1000):
    n = []
    for N in xrange(1001):
        z = N + alpha
        p = [ni / z for ni in n]
        p.append(alpha / z)
        k = numpy.random.choice(len(p), p=p)
        if k<len(n):
            n[k] += 1
        else:
            n.append(1)
        if N in target:
            data[target[N]].append(len(n))

for i, N in enumerate(labels):
    p = alpha / (numpy.arange(N) + alpha)
    m = p.sum()
    v = ((1 - p) * p).sum()
    print "%d: mean=%.2f(%.2f) sd=%.2f(%.2f)" % (N, numpy.mean(data[i]), m, numpy.std(data[i]), numpy.sqrt(v))

import matplotlib.pyplot as plt
plt.boxplot(data, labels=labels)
plt.show()

*1:正確には無相関で十分

2015-06-26

ディリクレ過程(中華料理店過程)のトピック数(テーブル数)の期待値を導出してみる #ぞくパタ

ぞくパタノンパラベイズ

「続・わかりやすいパターン認識」(以降「ぞくパタ」)の11章「ノンパラメトリックベイズモデル」を読んでいる。

ぞくパタはこの11章・12章のための本、と言ったらさすがに言いすぎなのかもしれないけど、そのつもりで読んでる人はけっこう多そう。
ノンパラベイズをしたかったら英語の論文読むしかない状態だったのが、日本語で読めるようになったというだけでも十分価値があるわけだが、ディリクレ過程と、無限次元ディリクレ分布や中華料理店過程との関係などもきちんとフォローされているし、ディリクレ過程とはどのようなふるまいをするものなのか、あれこれ実験して示してもくれていて、これは力作だなあと頭が下がる。

といっても、そもそも題材が本質的に易しくないので、これほどていねいに解説されてあっても、さらっと読んだだけではまったく意味はわからない。紙と鉛筆無しで理解できたら、ウン千人かに一人の天才以上だろう。
読書会もまもなくノンパラベイズに突入するが、それなりの覚悟を持って予習するのがおすすめ。

とまあ前振りはこれくらいで。
ぞくパタ 11章の p227 にて

CRP(中華料理店過程)では、客に使用されているテーブル数は、来客数 n の増加とともに増大し、その使用テーブル数の期待値 E[c] は、理論的には E[c] = O(αlog n) となることが知られている。

とあった。
テーブル数（つまりトピック数）の期待値が分かれば、集中度 α を決める目安になるので、どうやって求めるのかちょっと興味を持って探してみたら、英語 wikipedia の Chinese Restaurant Process のページに載っていた。

Chinese restaurant process - Wikipedia

(ぞくパタとは記号の使い方が異なるので注意)

が、式見た瞬間に導出方法がわかるくらい簡単なものだったので（答え見る前に自力でわかればよかったのだけどｗ）、せっかくだから紹介してみよう。

n 人の客が着席したときの、テーブル数を表す確率変数 c = c_n を考える。
また確率変数 X_k を「 k 人目の客が来たときに新しいテーブルに着いたら 1、すでに客のいるテーブルに着いたら 0 」（つまり k 人目の客のときのテーブル数の増分）とすると、 c は X_k の和に等しい。

$c = \sum_{k=1}^n X_k$

k 人目の客が新しいテーブルに着く確率は $\frac{\alpha}{k-1+\alpha}$ なので、

$E[X_k]=1\cdot\frac{\alpha}{k-1+\alpha}+0\cdot\frac{k-1}{k-1+\alpha}=\frac{\alpha}{k-1+\alpha}$

ここで、確率変数の和の期待値は、期待値の和になる(独立でなくても成立するが、今回は独立なのでどっちでもいい)ので、

$E[c] = \sum_{k=1}^n E[X_k] = \sum_{k=1}^n \frac{\alpha}{k-1+\alpha}$

とわかる。
さらに digamma 関数Ψの特性 $\Psi(z+1)=\Psi(z)+\frac1z$ を使えば $E[c]=\alpha\{\Psi(\alpha+n)-\Psi(\alpha)\}$ と表せる。実装や見積もりではこちらが速くて便利だろう。
クラスタ数（トピック数）はわからないとはいっても目星くらいはあるだろうから、この期待値がその目安となる数字を少し超えるくらいにαを選ぶと良さそう。

あとは E[c] = O(αlog n) であることを大雑把に示してみる。
といっても $\alpha\approx 1$ として、さらに和を積分で近似してしまえばあっさり出る*1。

$E[c]=\sum_{k=1}^n \frac{\alpha}{k-1+\alpha}\approx \sum_{k=1}^n \frac{\alpha}{k} \approx \int_1^n \frac{\alpha}{k}dk = \alpha\log n$

ちなみに、alpha = 1.0, n = 500 のとき(ぞくパタ 12章の実験の設定)、E[c] = 6.8 なのだが、αlog n = 6.2 とそれなりの近さ。
まあ元の式も十分簡単なので近似の意味はたいしてなさそうだけど、計算機を使わずに頭の中で目安を立てるくらいになら使えるかも。

*1:真面目にやるなら、ちゃんと上からおさえなきゃなんだろうけど、ごちゃごちゃするだけなのでネグる